We can now apply the conservation laws 
and 
to find the conservation equations. We have:
If we multiply by 
and use
and
we get
which gives
where 
is the derivative along the world line of the fluid.
The i components of give
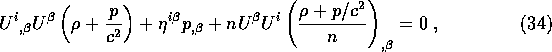
so in the MCRF [ 
] this equation is
Equation (33) is the energy conservation equation and equation (35) is the momentum conservation equation [ or acceleration equation ].
In the Newtonian limit 
and 
so in this case the
conservations equations become [ Assignment 4 ]
and
where we have used
